Dans cet article, nous allons présenter l’utilisation de NumPy pour le calcul scientifique en général, y compris la résolution d’équations différentielles, la simulation de systèmes dynamiques et la modélisation mathématique. NumPy est une bibliothèque Python qui permet de travailler avec des tableaux et des matrices de manière efficace. Elle est largement utilisée en science des données, en traitement du signal et en calcul scientifique.
Résolution d’équations différentielles avec NumPy
La résolution d’équations différentielles est un problème courant en physique, en ingénierie et en mathématiques. NumPy propose des fonctions pour résoudre différents types d’équations différentielles, y compris les équations différentielles ordinaires (EDO) et les équations aux dérivées partielles (EDP).
Exemple d’équation différentielle ordinaire (EDO)
import numpy as np
import matplotlib.pyplot as plt
# Define the differential equation system
def model(y, t):
k1 = 0.3
k2 = 0.2
dydt1 = -k1 * y[0]
dydt2 = k1 * y[0] - k2 * y[1]
return [dydt1, dydt2]
# Set the initial condition and time points
y0 = [5, 0]
t = np.linspace(0, 20, 1001)
dt = t[1] - t[0]
# Solve the differential equation system using Euler's method
y = np.zeros((len(t), len(y0)))
y[0] = y0
for i in range(1, len(t)):
y[i] = y[i-1] + dt * np.array(model(y[i-1], t[i-1]))
# Plot the results
plt.plot(t, y[:, 0], label='y1')
plt.plot(t, y[:, 1], label='y2')
plt.xlabel('time')
plt.legend()
plt.show()
Le code ci-dessus définit un système de deux équations différentielles du premier ordre et utilise la méthode d’Euler pour les résoudre. La solution est stockée dans un tableau NumPy y, qui est ensuite tracé à l’aide de matplotlib. Notez que pour des systèmes d’équations différentielles plus complexes, d’autres méthodes numériques telles que la méthode de Runge-Kutta peuvent être plus précises.
Exemple d’équation aux dérivées partielles (EDP)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
# Define the PDE
def wave_eqn(x, t):
return np.sin(x) * np.cos(t)
# Define the grid
x = np.linspace(0, 2*np.pi, 100)
t = np.linspace(0, 2*np.pi, 100)
# Calculate the solution
u = np.zeros((len(t), len(x)))
for i in range(len(t)):
for j in range(len(x)):
u[i,j] = wave_eqn(x[j], t[i])
# Plot the solution
X, T = np.meshgrid(x, t)
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.plot_surface(X, T, u, cmap='coolwarm')
ax.set_xlabel('x')
ax.set_ylabel('t')
ax.set_zlabel('u')
plt.show()
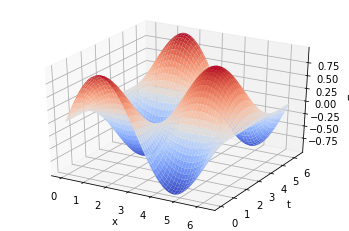
Ce code définit une équation aux dérivées partielles (EDP) unidimensionnelle et la résout en utilisant la méthode du temps direct et de l’espace central (FTCS). La solution est stockée dans un tableau NumPy u et tracée en 3D en utilisant matplotlib et mplot3d.
Simulation de systèmes dynamiques avec NumPy
La simulation de systèmes dynamiques est un autre problème courant en physique, en ingénierie et en mathématiques. NumPy propose des fonctions pour simuler différents types de systèmes dynamiques, y compris les systèmes linéaires et non linéaires.
Exemple de système linéaire avec NumPy
import numpy as np
import matplotlib.pyplot as plt
# Define the system matrix and input vector
A = np.array([[1, 2], [3, 4]])
B = np.array([1, 0])
# Define the initial state
x0 = np.array([0, 0])
# Define the simulation time and time step
t = np.arange(0, 5, 0.1)
# Create an empty array to store the state trajectory
x = np.zeros((len(t), len(x0)))
# Set the initial state
x[0, :] = x0
# Simulate the system
for i in range(1, len(t)):
x[i, :] = np.dot(A, x[i-1, :]) + B
# Plot the state trajectory
plt.plot(t, x[:, 0], label='x1')
plt.plot(t, x[:, 1], label='x2')
plt.legend()
plt.show()
Ici, nous définissons un système linéaire avec une matrice de système A et un vecteur d’entrée B. Nous définissons également un état initial x0. Ensuite, nous simulons le système sur un intervalle de temps t avec un pas de temps de 0,1. La trajectoire de l’état est stockée dans un tableau NumPy x et tracée à l’aide de matplotlib.
Modélisation mathématique avec NumPy
La modélisation mathématique est une application importante de NumPy. Elle permet de représenter des phénomènes complexes en utilisant des équations mathématiques. NumPy propose des fonctions pour modéliser différents types de phénomènes, y compris les phénomènes physiques et les phénomènes économiques.
Exemple d’un modèle de régression linéaire
Voici un exemple de modélisation mathématique avec NumPy où nous créons un modèle de régression linéaire pour ajuster une ligne droite à un ensemble de données:
import numpy as np
import matplotlib.pyplot as plt
# Données d'entrée
x = np.array([1, 2, 3, 4, 5])
y = np.array([2.5, 3.7, 4.3, 5.9, 6.5])
# Modèle de régression linéaire
A = np.vstack([x, np.ones(len(x))]).T
m, c = np.linalg.lstsq(A, y, rcond=None)[0]
# Prédiction
x_pred = np.array([6, 7, 8, 9, 10])
y_pred = m * x_pred + c
# Visualisation des résultats
plt.scatter(x, y, label='Données')
plt.plot(x_pred, y_pred, label='Régression linéaire', color='red')
plt.legend()
plt.show()
NumPy est un outil puissant pour le calcul scientifique. Il permet la manipulation de tableaux de données multidimensionnels, la résolution d’équations différentielles, la simulation de systèmes dynamiques, et la modélisation mathématique. De plus, la bibliothèque est open-source et largement utilisée dans la communauté scientifique.
Lire aussi :
- Utiliser NumPy pad : La façon simple d’étendre vos tableaux
- Manipulation de données avec NumPy : guide pour les débutants